A Different Way to View Imaginary Numbers Better Explained

The name of the imaginary numbers includes the impression of the numbers are in the imagination and they do not actually exist. Examples of Imaginary Numbers.

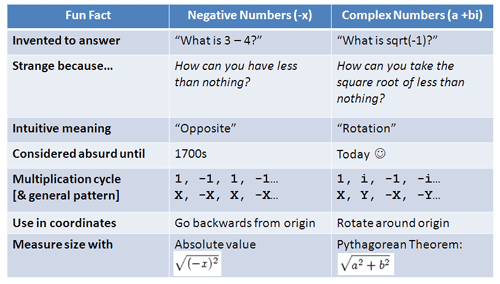
A Visual Intuitive Guide To Imaginary Numbers Betterexplained

The name of imaginary numbers.

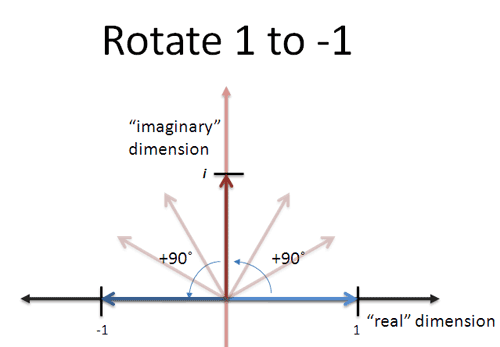
. However they exist in the context of a different number system something different from the number systems we are used to. The best way to explain imaginary numbers would be to draw a coordinate system and place the pen on the origin and then draw a line of length 3. Consider abicdi It becomes.

Learn to understand i the imaginary number as a rotation. This must be wrong but I dont see why. Now since an imaginary number involves looking to your side its the same as turning 90 degrees.

The imaginary number exists almost as same as rotational transformation existing well. The question anyone would ask will be where to or which direction. Lets start with the following calculation.

Not imaginary numbers but imaginary geometry. However the imaginary number is rotational transformation as I explained it in this page. Taking the squares of these numbers sheds some light on how they relate to the real numbers.

This approach will help when we cover imaginary numbers that foul beast which has befuddled many students. Little insights help bigger ideas click. If you tell them to go right they reach the point 3 0.

Subtraction of Numbers Having Imaginary Numbers. 2 8 1 3 8 2 6 8 2 1 6 64 1 6 2. Imaginary and Complex Numbers.

What relevance do imaginary numbers have to the real world. I know which approach keeps my curiosity and enthusiasm. Imaginary numbers are two dimensional number what could be the two dimension in real life it is the magnitude and time magnitude is one dimensional and time is another dimensional magnitude is different for each time for example for a sine wave magnitude at time 0 is 0 where as time at 2pif1t14 pi2 2pi is the circumference of a circle frequency.

If you turn 180 degrees twice you are looking back at your original direction so -1 -1 1. Here abi-cdi a-c ib-d. If you look forward and multiply by -1 then thats the same as turning 180 degrees.

But in electronics they use j because i already means current and the next letter after i is j. When studying linear algebra matrices you can view multiplication as a type of transformation scaling rotating skewing instead of a bunch of operations that change a matrix around. Learning isnt about memorizing facts to pass a test.

One in which number means a measurement of how many items are in a set a second one in which number means a relative measurement of the sizes of two sets a third one in which number means a ratio of sizes of two sets and a fourth one in which number means a measurement of a continuous. Youll probably find it helpful to open another window on your web browser and view the two of them side by side. The square root of minus one 1 is the unit Imaginary Number the equivalent of 1 for Real Numbers.

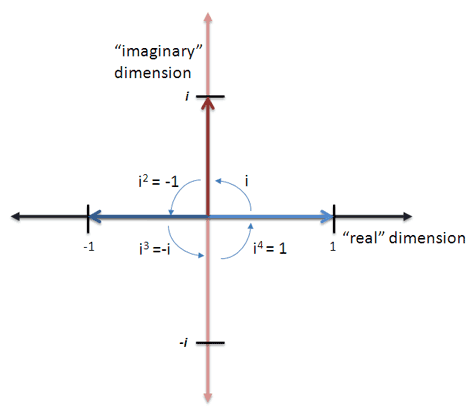
Its about unlocking the joy of discovery when an idea finally makes. The simplest way to understand imaginary numbers is to interpret multiplication of 1 -1 and -1 or as Gauss says direct inverse and lateral units as. So ii -1.

Okay I know about four different number systems. It turns out that theres a way to get the solutions provided one can solve the quadratic equation a r2. The simplest way to understand imaginary numbers is to interpret multiplication of 1 -1 and -1 or as Gauss says direct inverse and lateral units as.

By taking multiples of this imaginary unit we can create infinitely many more pure imaginary numbers. Multiplication of Numbers Having Imaginary Numbers. Can you take the square root of 1.

One way to engage with geometry is to consider Kanizsa figures such as the one below the Kanizsa triangle. Imaginary numbers involve walking to the side. This argument is patterned after the above argument that fractions exist.

Kanizsa figures challenge your perceptions because you see whats not actually there. Imaginary numbers dont exist but so do negative numbers. If we examine circular motion using trig and travel x radians.

I think that we had better explain the imaginary numbers in the view point of the matrices. It means grouping all the real terms separately and imaginary terms separately and doing simplification. So some mathematicians decided to define it so that you get the imaginary numbers if you take the square root of a negative number.

The learning strategy is the ADEPT Method. In mathematics the symbol for 1 is i for imaginary. One interesting quirk that arises that you need calculus to show easily is that e ix cos x isin x.

At 0 on the x -axis a y -axis can be drawn with. Moment and then the specifics. It gives two formulas which explain how to move in a circle.

The issue is the existence of the mysterious quantity i since imaginary numbers are just multiples of i. Intrigue and curiosity should be a part of everybodys learning. But this would conceal some wonderful underlying mathematics.

Answer 1 of 3. In mathematics the symbol for 1 is i for imaginary. By Rachael Horsman 23 November 2016.

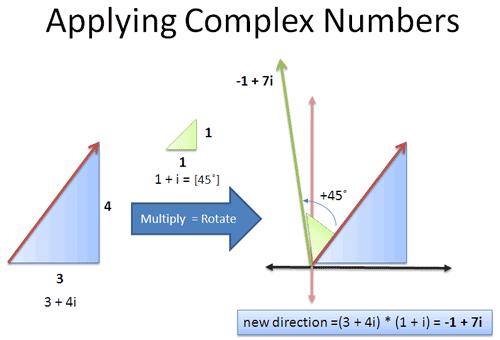
Is a clever way to smush the x and y coordinates into a single number. Especially in fields like physics and electrical engineering getting comfortable with imaginary numbers aka complex numbers having both a real and an imaginary component and using them can reduce a whole page full of calculations involving sines and cosines to one or two l. A big hole in algebra is that roots of negative numbers dont exist.

Okay now weve seen that imaginary numbers exist. In other words we want to see that there exists some number which when squared gives. Eulers formula is the latter.

I enjoyed this short summary by the user pdpi describing the motivation behind the concept of complex and imaginary numbers When I teach this I force students to go back to earlier sets that were not closed under our operations. Better Explained focuses on the big picture the Aha. The brutal answer would be that you should never write a p when a is negative.

For example and are all examples of pure imaginary numbers or numbers of the form where is a nonzero real number. When cdi is subtracted from abi the answer is done like in addition. Cos x is the x-coordinate horizontal distance sin x is the y-coordinate vertical distance The statement.

Reddits explainlikeimfive or ELI5 subreddit has many great descriptions that describe complex concepts in simple ways.

A Visual Intuitive Guide To Imaginary Numbers Betterexplained

A Visual Intuitive Guide To Imaginary Numbers Betterexplained

A Visual Intuitive Guide To Imaginary Numbers Betterexplained